- News
- Reviews
- Bikes
- Accessories
- Accessories - misc
- Computer mounts
- Bags
- Bar ends
- Bike bags & cases
- Bottle cages
- Bottles
- Cameras
- Car racks
- Child seats
- Computers
- Glasses
- GPS units
- Helmets
- Lights - front
- Lights - rear
- Lights - sets
- Locks
- Mirrors
- Mudguards
- Racks
- Pumps & CO2 inflators
- Puncture kits
- Reflectives
- Smart watches
- Stands and racks
- Trailers
- Clothing
- Components
- Bar tape & grips
- Bottom brackets
- Brake & gear cables
- Brake & STI levers
- Brake pads & spares
- Brakes
- Cassettes & freewheels
- Chains
- Chainsets & chainrings
- Derailleurs - front
- Derailleurs - rear
- Forks
- Gear levers & shifters
- Groupsets
- Handlebars & extensions
- Headsets
- Hubs
- Inner tubes
- Pedals
- Quick releases & skewers
- Saddles
- Seatposts
- Stems
- Wheels
- Tyres
- Health, fitness and nutrition
- Tools and workshop
- Miscellaneous
- Tubeless valves
- Buyers Guides
- Features
- Forum
- Recommends
- Podcast
feature
Does a heavier cyclist descend hills quicker? We strapped weights to ourselves to find out
It sounds obvious that a heavy rider will descend quicker than a light one. After all, gravity is your friend when barrelling downhill... but how much difference does it make? In an attempt to find out, we strapped 8kg to ourselves and set off to do some garage science!
Heavier riders descend quicker right? It's been ingrained in us since secondary school physics lessons. Well, that's what we thought, but look at recent descending masterclasses and it's the light riders often leading the way. Take Tom Pidcock for example, both one of the lightest and fastest descenders in the peloton, and it kind of upsets this theory.
> 14 expert tricks for better descending
> How Fast!? We take a look at Tom Pidcock's Alpe d'Huez conquering Strava file
Does this mean that weight has a far smaller impact on descending than we might have previously thought?
The test
Whilst watching Ed struggle home from the supermarket with 8kg of water, an idea popped into my head. Firstly, I wondered if I could beat him up a hill if he was 8kg heavier, and secondly I wondered if it could make him beat me down one...
To find out once and for all how much difference weight makes when descending, we found a suitable hill and devised a plan for two tests. Test number one would involve timed runs down a steep hill with and without the additional water, and the second included a roll back up the other side of the tip until Ed ground to halt. In the first test the lowest average time would win, and in test two the winner would be the one who travelled the farthest distance.
We decided that strapping the weight to Ed's front would have less of an impact on his aerodynamics than if it was on his back. It also better simulates a larger/heavier rider as this does tend to be where many of us hold that additional weight.
Results, part 1 (the steep descent)
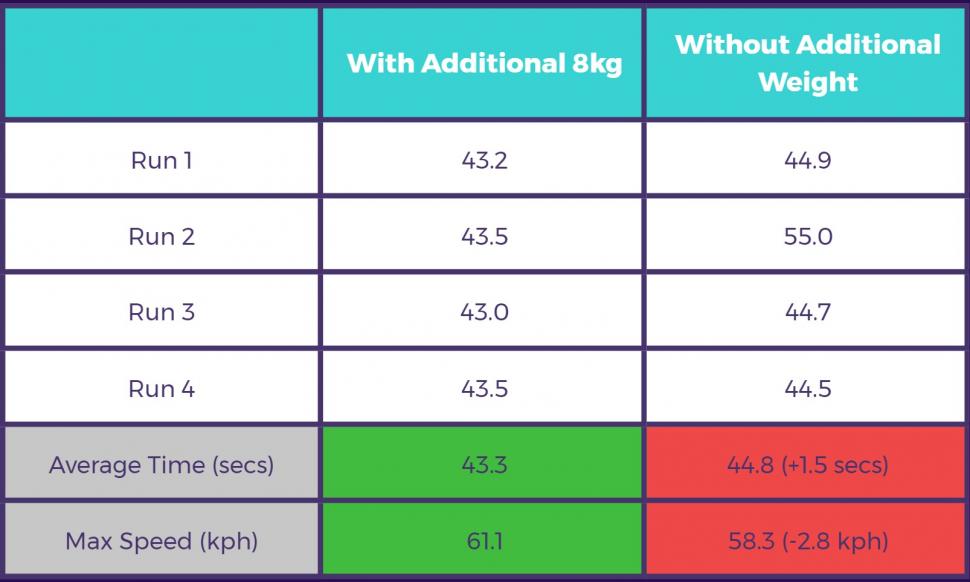
We start off on the timed runs down the steeper of the two descents. According to Strava this had an average gradient of -10% and lasted around 40 seconds.
> Hitting 100kph on a bike — what does it take to break this elusive cycling speed barrier?
To make the results as reliable as possible, Ed wasn't allowed to pedal at any point during the descents. He got a TT-style start to avoid having to push off the line, and took the same line through the one corner each time. He also tried as hard as possible to maintain the same position throughout the testing, and we did it on the stillest day possible to try and avoid any wind gusts that could throw the results.
For the first test, Ed did a total of eight attempts, each three-quarters of a kilometre long, four with the 8kg of water and four without. Overall he was quicker (drum roll, please)... WITH the additional weight; but not by as much as you might think.
That means that the additional 8kg made Ed on average 1.5 seconds faster on our descent. That might not sound like a lot, but it is over 3% difference.
It is worth noting, however, that the weight would have less of an effect on a shallower descent, or indeed if there were more corners where braking and acceleration were required.
Results, part 2 (rolling to a halt)
> How hard is it to train like a pro cyclist? Spending a week riding like an elite
For the second test, we set Ed off down the same descent, but instead of stopping at the bottom he carried on rolling up the other side of the dip until he ground to a halt. We then measured the distance he reached each time, again four times with the 8kg of additional weight and four without.
To Ed's surprise, this time he performed better without the water strapped to him, stopping on average two meters further than when bottled up.
Why is this?
There are two main forces acting on a rider and their bike when cycling downhill. As Ed isn't pedalling, any forward acceleration is due to gravity. As you’ll remember from back in school F=ma where:
Force = mass x acceleration
Therefore, when we make Ed heavier the m in the equation gets bigger, so the force pushing him forwards gets bigger too.
However, the second major force to consider is air resistance, which opposes a rider's motion. The faster you go or the less aerodynamic you are the bigger this force gets.
As we strapped the water to Ed's front and given the results, it's unlikely that we changed Ed's drag coefficient significantly. This is why on the timed descent, Ed was quicker when carrying the additional weight.
However, when we then threw in the ascent on the other side it’s clear that the weight has more of a negative impact going up the hill than going down it, otherwise he would have travelled further.
Because air resistance has a non-linear relationship with speed, the additional weight has a far bigger impact when travelling at lower speeds, i.e uphill. Unfortunately, for many of us, this is the area we want to improve and is also where many races (both professional and on the club run) get decided.
> Power-to-weight ratio: what is W/kg, and why does it matter?
It’s for this reason that nearly all the successful general classification riders look in such depth at improving their power-to-weight ratios, and are seriously lean for target events.
Conclusion
So, does a heavier rider descend quicker? Well, yes, in a straight line at least. However, as we previously discussed your weight pales into insignificance when compared to aerodynamic drag. Therefore, if you want to get faster at descending, our advice is not to hit the all-you-can-eat buffet but rather work on your position and ditch the flappy clothing.
It's also worth noting that any advantage on the descents that you do get from being heavier will have far more of a negative impact when the road heads upwards! If you want a better idea of how much weight can slow you down, when climbing then you can check out our analysis of Tadej Pogacar's fateful climb from last year's Tour De France below.
> Did disc brakes get Pogacar dropped? How much difference does that extra 300g make?
Let us know what garage science you’d like us to do next time in the comments section below!
Jamie has been riding bikes since a tender age but really caught the bug for racing and reviewing whilst studying towards a master's in Mechanical engineering at Swansea University. Having graduated, he decided he really quite liked working with bikes and is now a full-time addition to the road.cc team. When not writing about tech news or working on the Youtube channel, you can still find him racing local crits trying to cling on to his cat 2 licence...and missing every break going...
Latest Comments
- chrisonabike 1 sec ago
Just get them to walk a treadmill - or better, ride exercise bikes to power path lighting.
- AidanR 36 min 4 sec ago
So his advisers were trying to move funds around to cover losses, but in a way that needlessly created additional liabilities? It would have been...
- levestane 37 min 11 sec ago
Reading this and watching the GCN review has made me realise that, for me, it's not the bike being steel (narrow tubes) that is the critical...
- Rendel Harris 44 min 32 sec ago
Given that the property is private a more elegant and less vandalistic approach would be to lock the bikes away somewhere and contact Lime to...
- Rendel Harris 56 min 44 sec ago
God yes, awful in every way, feeble light, gobbled batteries and so un-weatherproof that you had to take the batteries out and wipe out the innards...
- David9694 2 hours 10 min ago
Try https://www.thetelegraphandargus.co.uk/news/24739976.overturned-car-chat...
- chrisonabike 2 hours 35 min ago
Yes - or:...
- Bungle_52 3 hours 11 min ago
Tweak no 1 then. The tag would need to beep at around 15mph getting more frequent as it approaches 20. It would come with an advisory note to...
- mark1a 4 hours 49 sec ago
That will be along in a week or so in the annual reboot of the "All I want for Christmas is... not this" article along with the Park Tool pizza...
- hawkinspeter 4 hours 19 min ago
The problem with most jeans (i.e. not cycling designed ones) is that they've got the seam where it can intefere/chafe with the saddle. Also, cotton...









Add new comment
88 comments
I'm sorry i upset you so much.
You could try reading Basic Engineering Mechanics Explained (Gregory Pastoll). Let me know if you need any help with the longer words.
Watch this please https://youtu.be/_mCC-68LyZM veritasium is very good at explaining things.
Any credibility as an aerodynamicist disappeared with talk of a "ferring"!
A child knows this.
Thanks... Did you watch the vid???
Dyslexic. Spelling not my strong point, sorry if that makes me less credible to you.
This might help you https://youtu.be/_mCC-68LyZM
Yes that video debunks most of what you've said.
And you would be viewed as a useless pillock in places in places where they excelled.
BTW a huge amount about knowing how the 'real world' works can be explained by physics.
Quite - physics is very much an investigation into how the 'real world' works
Is a ton of climbers lighter than a ton of sprinters, though? (Presumably "yes, when the climbers have got ahead and are higher up the mountain")
(Presumably "yes, when the climbers have got ahead and are higher up the mountain")
What about when the climbers are descending and the sprinters are still climbing though?
Good point, I was using way too simple a model. - We should also factor in rates of perspiration and evaporation, differential tyre and brake mass loss, oh, and can anyone reach relativistic speeds on descent?
Anyone can reach relativistic speeds on a descent, but it does require a very dense object such as a neutron star or black hole.
So your old skinny steel tube bike is more aero than modern chunky aero road bikes???? Wow...
That's mainly due to the profile of the tubes. Skinny steel bikes typically have circular tube profiles whereas modern CF bikes tend towards having a truncated aerofoil shape.
I am surprised that you believe that having a larger frontal cross-section leads to better aerodynamics - you should test that out by cycling with a cardboard box taped to your handlebars and comparing your speed/effort with having the same carboard box flat-packed and held sideways (i.e. thinnest dimension towards the front).
I don't, aerodynamics is hard. The reason aerofoils are fast has to do with how the air is disturbed. Different people are very different aerodynamically. Skinny people like andy shleck where very un aero compared to leaa skinny people like Fabian. Obs it got more to do with arm length then fat content. I'm telling you that it's not mass it's all inertia for a rolling start and aerodynamics that makes some riders go down hill faster.
This is a worryingly inaccurate statement for someone claiming to have an O level, let alone a Phd in physics. Firstly it has nothing to do with fat versus thin, it is about heavy versus lighter so you didn't even read the question.
So take two cyclists of the same shape, therefore having the same drag coefficient (Cd), but differing in height by 10%. 10% height difference given same shape and density translates one being 32% heavier than the other, therefore the force pulling him down the hill is 32% higher. The aerodynamic drag at any given speed (Cd * frontal area) only increases by 21%. Therefore the speed at which the two forces balance out is higher for the heavier rider, and he will reach a higher terminal velocity.
*Note that although Cd is expressed as per unit frontal area it takes into account the 3d shape of an object, and is specifically used for comparing drag of different shapes irrespective of their size, so two riders of the same shape but different size, will indeed have the same drag coefficient.
Nope your right I forgot about terminal velocity. The heavier rider has a higher terminal velocity. I got court up with people not thinking about inertia. What i have been saying applies until the one of the two objects (light / heavy) reaches terminal velocity. At that point the lighter one (assuming same Cd) stopped accelerating. So if you start pulling away for your riding buddys at the top of the hill or straight away it's not your weight just how aero u are. Depends on the slope as well.
Nope, more "bad physics". Aero doesn't just step in at terminal velocity. Right from the off, the aero drag is resisting the gravitational force, more so on the lighter cyclist (as already explained due to his larger relative frontal area in relation to mass), so the heavier rider accelerates faster, in addition to reaching a higher terminal velocity.
(With regard to your ramblings on inertia, perhaps you should read the article again. I draw your attention to the bit about the route not having much in the way of bends, so braking and acceleration (where intertia comes into play) were not major factors.)
Now that we are agreed on that, the polite thing to do would be to apologise to the author.
Looking forward to next week's hard hitting expose on whether ursine faeces can be found in sylvan enviroments
(assume there is a typo and that the slowest run was 45seconds not 55seconds)
Anybody who has ever tried to keep up with a tandem on a descent wouldn't need to do this experiment, but it sounds like you had fun, so well done.
Of course, the problem is that a tandem also has the capability to ascend well assuming you have 2 reasonable riders.
New just in physics gonna physic.
What was the starting speed for each run as this will have an effect on measured time differences?
If starting from a standing start, then the differences will be smaller, as at lower speeds air resistance would play a smaller part and acceleration would be similar. The differences would only start to mount up once air speed is significant, so for a good chunk of each run, there would be no differences.
I'd be interested to see the results if each run started at say 40kph.
Anecdotely, I'm a fat sprinter and I descend quicker than most. I always tell people I've learnt to descend fast as I need to catch back up after being dropped on the hills, however the reality is its just gravity working in my favour.
My old club used to have a downhill championship every year: same hill, drivetrain disconnected. It was an easy descent followed by a gentle incline. No one under 90kg ever won it.
No one under 90kg ever won it
I think this experiment is quite strong evidence in the debate. I always overtake my lightweight daughter just rolling downhill, and she's on a pretty good Whyte which is classier than my worn gravel bike in every respect but is still on 700c. I must have an absolute wind resistance higher than hers, my absolute force of gravity (weight) is considerably greater, but so is my mass. This must all be quite complicated
No, it's quite simple. You'll keep getting quicker until the forces cancel each other out (wind resistance versus gravity). That is true regardless of mass. But of course gravity pulls stronger on the more massive object (witness the scales of truth), so wind resistance (hence speed) must be greater before they reach equilibrium.
Yes, but greater in direct proportion. Since acceleration is given by the one divided by the other, and they are in direct proportion, the gravitational acceleration remains the same regardless of mass. Were it not for wind resistance the two of you would match each other's speed exactly.
Pages