- News
- Reviews
- Bikes
- Accessories
- Accessories - misc
- Computer mounts
- Bags
- Bar ends
- Bike bags & cases
- Bottle cages
- Bottles
- Cameras
- Car racks
- Child seats
- Computers
- Glasses
- GPS units
- Helmets
- Lights - front
- Lights - rear
- Lights - sets
- Locks
- Mirrors
- Mudguards
- Racks
- Pumps & CO2 inflators
- Puncture kits
- Reflectives
- Smart watches
- Stands and racks
- Trailers
- Clothing
- Components
- Bar tape & grips
- Bottom brackets
- Brake & gear cables
- Brake & STI levers
- Brake pads & spares
- Brakes
- Cassettes & freewheels
- Chains
- Chainsets & chainrings
- Derailleurs - front
- Derailleurs - rear
- Forks
- Gear levers & shifters
- Groupsets
- Handlebars & extensions
- Headsets
- Hubs
- Inner tubes
- Pedals
- Quick releases & skewers
- Saddles
- Seatposts
- Stems
- Wheels
- Tyres
- Health, fitness and nutrition
- Tools and workshop
- Miscellaneous
- Tubeless valves
- Buyers Guides
- Features
- Forum
- Recommends
- Podcast
feature
Does a heavier cyclist descend hills quicker? We strapped weights to ourselves to find out
It sounds obvious that a heavy rider will descend quicker than a light one. After all, gravity is your friend when barrelling downhill... but how much difference does it make? In an attempt to find out, we strapped 8kg to ourselves and set off to do some garage science!
Heavier riders descend quicker right? It's been ingrained in us since secondary school physics lessons. Well, that's what we thought, but look at recent descending masterclasses and it's the light riders often leading the way. Take Tom Pidcock for example, both one of the lightest and fastest descenders in the peloton, and it kind of upsets this theory.
> 14 expert tricks for better descending
> How Fast!? We take a look at Tom Pidcock's Alpe d'Huez conquering Strava file
Does this mean that weight has a far smaller impact on descending than we might have previously thought?
The test
Whilst watching Ed struggle home from the supermarket with 8kg of water, an idea popped into my head. Firstly, I wondered if I could beat him up a hill if he was 8kg heavier, and secondly I wondered if it could make him beat me down one...
To find out once and for all how much difference weight makes when descending, we found a suitable hill and devised a plan for two tests. Test number one would involve timed runs down a steep hill with and without the additional water, and the second included a roll back up the other side of the tip until Ed ground to halt. In the first test the lowest average time would win, and in test two the winner would be the one who travelled the farthest distance.
We decided that strapping the weight to Ed's front would have less of an impact on his aerodynamics than if it was on his back. It also better simulates a larger/heavier rider as this does tend to be where many of us hold that additional weight.
Results, part 1 (the steep descent)
We start off on the timed runs down the steeper of the two descents. According to Strava this had an average gradient of -10% and lasted around 40 seconds.
> Hitting 100kph on a bike — what does it take to break this elusive cycling speed barrier?
To make the results as reliable as possible, Ed wasn't allowed to pedal at any point during the descents. He got a TT-style start to avoid having to push off the line, and took the same line through the one corner each time. He also tried as hard as possible to maintain the same position throughout the testing, and we did it on the stillest day possible to try and avoid any wind gusts that could throw the results.
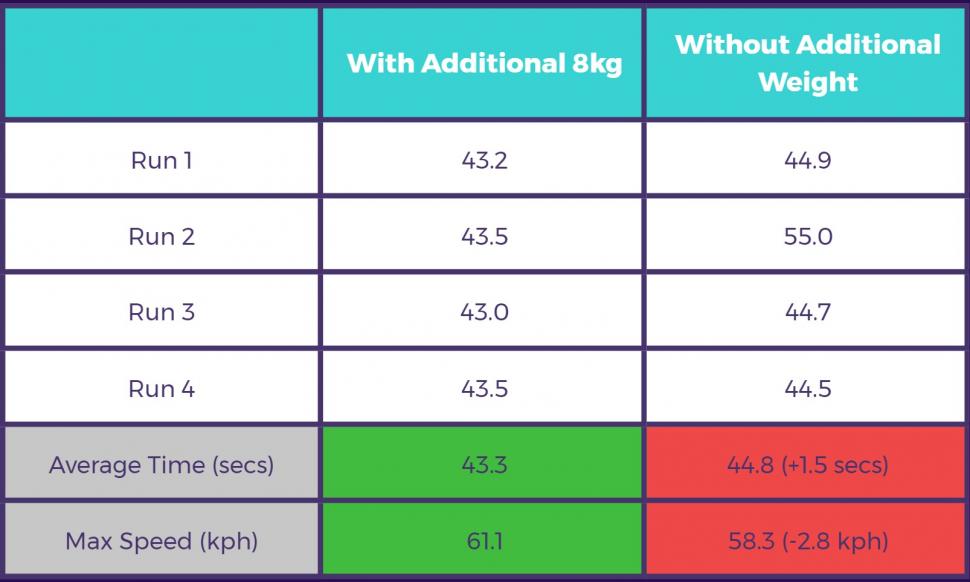
For the first test, Ed did a total of eight attempts, each three-quarters of a kilometre long, four with the 8kg of water and four without. Overall he was quicker (drum roll, please)... WITH the additional weight; but not by as much as you might think.
That means that the additional 8kg made Ed on average 1.5 seconds faster on our descent. That might not sound like a lot, but it is over 3% difference.
It is worth noting, however, that the weight would have less of an effect on a shallower descent, or indeed if there were more corners where braking and acceleration were required.
Results, part 2 (rolling to a halt)
> How hard is it to train like a pro cyclist? Spending a week riding like an elite
For the second test, we set Ed off down the same descent, but instead of stopping at the bottom he carried on rolling up the other side of the dip until he ground to a halt. We then measured the distance he reached each time, again four times with the 8kg of additional weight and four without.
To Ed's surprise, this time he performed better without the water strapped to him, stopping on average two meters further than when bottled up.
Why is this?
There are two main forces acting on a rider and their bike when cycling downhill. As Ed isn't pedalling, any forward acceleration is due to gravity. As you’ll remember from back in school F=ma where:
Force = mass x acceleration
Therefore, when we make Ed heavier the m in the equation gets bigger, so the force pushing him forwards gets bigger too.
However, the second major force to consider is air resistance, which opposes a rider's motion. The faster you go or the less aerodynamic you are the bigger this force gets.
As we strapped the water to Ed's front and given the results, it's unlikely that we changed Ed's drag coefficient significantly. This is why on the timed descent, Ed was quicker when carrying the additional weight.
However, when we then threw in the ascent on the other side it’s clear that the weight has more of a negative impact going up the hill than going down it, otherwise he would have travelled further.
Because air resistance has a non-linear relationship with speed, the additional weight has a far bigger impact when travelling at lower speeds, i.e uphill. Unfortunately, for many of us, this is the area we want to improve and is also where many races (both professional and on the club run) get decided.
> Power-to-weight ratio: what is W/kg, and why does it matter?
It’s for this reason that nearly all the successful general classification riders look in such depth at improving their power-to-weight ratios, and are seriously lean for target events.
Conclusion
So, does a heavier rider descend quicker? Well, yes, in a straight line at least. However, as we previously discussed your weight pales into insignificance when compared to aerodynamic drag. Therefore, if you want to get faster at descending, our advice is not to hit the all-you-can-eat buffet but rather work on your position and ditch the flappy clothing.
It's also worth noting that any advantage on the descents that you do get from being heavier will have far more of a negative impact when the road heads upwards! If you want a better idea of how much weight can slow you down, when climbing then you can check out our analysis of Tadej Pogacar's fateful climb from last year's Tour De France below.
> Did disc brakes get Pogacar dropped? How much difference does that extra 300g make?
Let us know what garage science you’d like us to do next time in the comments section below!
Jamie has been riding bikes since a tender age but really caught the bug for racing and reviewing whilst studying towards a master's in Mechanical engineering at Swansea University. Having graduated, he decided he really quite liked working with bikes and is now a full-time addition to the road.cc team. When not writing about tech news or working on the Youtube channel, you can still find him racing local crits trying to cling on to his cat 2 licence...and missing every break going...
Latest Comments
- JLasTSR 6 min 46 sec ago
Since most of.my clothes come.from.charity shops.or the eBay nearly for.nothing clothing section I don't tend.to.worry if they wear out, I am also...
- David9694 21 min 37 sec ago
Someone, in the name of research, ought to place an order of some of this stuff. ...
- chrisonabike 52 min 10 sec ago
Just get them to walk a treadmill - or better, ride exercise bikes to power path lighting.
- AidanR 1 hour 28 min ago
So his advisers were trying to move funds around to cover losses, but in a way that needlessly created additional liabilities? It would have been...
- levestane 1 hour 29 min ago
Reading this and watching the GCN review has made me realise that, for me, it's not the bike being steel (narrow tubes) that is the critical...
- Rendel Harris 1 hour 36 min ago
Given that the property is private a more elegant and less vandalistic approach would be to lock the bikes away somewhere and contact Lime to...
- David9694 3 hours 2 min ago
Try https://www.thetelegraphandargus.co.uk/news/24739976.overturned-car-chat...
- chrisonabike 3 hours 27 min ago
Yes - or:...
- Bungle_52 4 hours 3 min ago
Tweak no 1 then. The tag would need to beep at around 15mph getting more frequent as it approaches 20. It would come with an advisory note to...









Add new comment
88 comments
Well done, yes this is correct! Inertias mass dependance cancels out gravity's mass dependance.
Rolling down a straight hill, the physics seem reasonably clear cut (some commentors seem a bit confused, but Sriracha's got the right idea).
But obviously Tom Pidcock et al. aren't rolling down straight hills. There are corners, there is braking and there is acceleration (actually those are all forms of accerleration). I would be interested to know how weight affects those things. On the one hand a lighter rider should require less force to slow down/corner/speed up, but on the other hand if the limiting factor is tyre grip, a heavier rider may create more friction and therefore be able to apply a greater force.
Well Jamie Williams obviously failed physics in school. Everything dropped accelerates at the same rate which is the acceleration due to gravity. Heavier objects with the same shape as lighter objects will have a higher terminal velocity.
You could also negate the aerodynamic effect of the water bottle by running tests with it full and empty and that 55s is an obvious outlier which should be ignored.
I think Jamie has a better grasp of the subject than you. Objects do not accelerate at the same rate. That's true in a vacuum, but in real life there are many types of drag that affect how quickly an object accelerates.
The writer does seem to have reached approximately the right conclusions, but appears to be a little muddled by the underlying physics. Down hill with greater mass but approximately the same air resistance, velocity of the heavier rider will likely be higher, but if you consider the additional gravitational potential energy they possessed at the top of the hill, at the bottom, because of the drag forces being higher at higher velocities and related to the square of the velocity, the proportion of their lost gravitational potential energy converted to kinetic energy by the rider with greater mass will be lower. They go faster, but not fast enough to overcome the burden of the additional mass they are carrying on a subsequent climb. Of course there are also all the complications of control at higher speeds that come with greater mass.
Festina is right, Jamie is wrong. I'm a theoretical physicist. The acceleration is the same and has no dependency on weight as the inertial force of the mass has to be overcome to more the object. These two masses cancel out. So all objects accelerate as the same rate. Yes the rest is due to aerodynamics. That is the effect that makes the times different. Rolling resistance is dependent on mass but that's the only way mass has an effect on this system. Terminal velocity is reached when the air resistance matches the acceleration due to gravity. Hence it's all about the shape not the weight.
It's not the heavier nor the more aerodynamic rider who descends faster, it's the braver one with more confidence (or blind faith) in their brakes and what's around the corner, both in terms of road surface and other road users.
So 8kg represents about a 10% increase in the total of rider, clothes and bike. This gives a 3% increase in speed. Which doesn't sound out of kilter with diminishing returns in these things.
I read somewhere a long time ago to increase the speed of a ship by 1 knot requires a doubling of horsepower.
Great article, thank you! This came up in a comment section here recently, and I've been thinking about it since.. I know it's unrealistic, but I want more data! Different size riders, and I'd like to see more variation in the course too to start! I'm also curious how much cornering is effected by weight, I'm assuming lighter would be more nimble, but I think we need a new article please!
I'm surprised anyone's surprised (that you descend faster if heavier).
My weight has fluctuated between 60kg and 68kg and, riding the same bike up and down the same hill, the extra weight makes me much faster down (let's not talk about the up).
Now, I just need to find someone to open a pie-shop at the top ...
Surely weight plays a big part.
If you really want to descend fast on anything other than closed roads the size of your bollocks and therefore their weight plays a huge part.
I don't like to brag, but I'm a bit of a demon at the descending malarkey.
As it's not April 1st, I'll bite.
On average you'd expect smaller, lighter riders to descend faster.
F=ma, so acceleration = force divided by mass.
Gravitational force is proportional to mass (double the mass, double the gravitational pull) so acceleration under gravity is a constant for any mass: approx 9.8 meters per second squared near the earth's surface.
In a vacuum, a feather will fall at the same rate as a 10kg cannon ball, in air the feather, with it's large surface area incurs a lot of drag, and falls much slower than the cannon ball.
A smaller, lighter rider will, on average, have a smaller frontal area, incurring less drag, and so will accelerate faster (potentially reaching a higher terminal velocity), even though the gravitational force is the same as for larger riders.
I would guess that the strapped-on water container, did affect the drag coefficient of the test rider - it may have been a fairer test if the experimenters had strapped on an empty water container for the control.
The important point is the aerodynamics of the two. A rider that's twice as heavy will have twice the force accelerating them, but is unlikely to present twice the aero drag and so will be pushing through the air quicker.
It's the same principle as terminal velocity and if you compare a 10kg cannon ball with a slightly smaller football, the 10kg cannon ball will have a faster terminal velocity.
I was told it's surface area relative to mass, assuming the same shape, will determine terminal velocity. I think heavier things will fall faster as a lot the inside is kind of protected (I guess slip streaming) from the air resistance.. So a 1kg cannon ball will fall (I assume roll too) faster in an atmosphere, than 1000 1g balls made from the same cannonball.
TL;dr Speed increases until wind resistance equals the force due to gravity, which is greater for the heavier rider.
Acceleration = force/mass.
Force (i.e. weight) is in proportion to mass so both riders experience the same acceleration due to gravity.
So ignoring air (and other) resistances, all riders experience the same acceleration and their speeds remain in lockstep.
But resistances can't be ignored. A rider will stop accelerating when there is net-zero force, the speed where resistances (a function of speed) equal the force due to gravity, at which point they hold their current speed.
The heavier rider enjoys a greater force due to gravity (i.e. they weigh more), so they must be going faster before resistances balance it out.
That assumes both riders present similar aerodynamic characteristics.
My observation, riding with a heavier person, is that they easily descend faster than me - no contest. They also ascend much faster, but I put that down to them riding an e-bike!
The gravitational force is higher for an object with more mass, they also have proportionally greater inertia due to that mass, consequently in a gravitational field in the absence of resisting force they accelerate at the same rate.
"Heavier riders descend quicker right? It's been ingrained in us since secondary school physics lessons. " - Um... no? As a one time physics teacher I seem to remember teaching 'All objects fall at the same rate in a vacuum, regardless of mass' -Galileo demonstrated it (without the vacuum) -apocryphally from the Leaning Tower of Pisa. Neil Armstrong did it on the moon, with the vacuum.
This. The question I want answered is, given knowledge of physics dating back 400 years, why does a heavier person descend faster?
The riders' stop getting quicker only when their air resistance exactly opposes their gravity. The heavier rider has more gravity, so they need to be going faster for their air resistance to be equal (and opposite) to their gravity. Only then does their speed level off.
You would have thought that would have added extra unnecessary weight but I guess he was a neat freak.
It's necessary - otherwise when you try to dust off the cheese-mites what with the low gravity it'd quickly be like a sandstorm.
smallest vacuum I've ever seen
And, I hope you noticed, he wore a helmet.
I've never ridden a bike on the moon. so air resistance is a real factor.
Absolutely -my comment was addressing the 'ingrained since seconfdary school physics' point. On the terminal velocity question there are (post high school) formulae that are hard to write here along the lines of V =Sqr rt((2m.g.sin theta -mu.k/(rho.A.Cda)) where terms have ther usual meannings (and combining mechanical friction and rolling resistance into mu.k.) One of the fun things is terminal V would be airspeed not ground speed. The (much lower) frictional forces (mu.k) would of course be groundspeed not airspeed related. Upshot is that if all else is equal, terminal velocity is proportional to the square root of mass.
True ... except that it was David Scott on the Apollo 15 mission
oops!
8kg isn't that much of a weight penalty. I remember a time when I overtook a chap probably twice my weight on a hill. On the downhill on the other side he went past me (not pedalling) and I could not catch him regardless of how hard I pedalled. Double the weight and the difference becomes much more pronounced!
Pages